Understanding of average in mathematics involves calculating a set of numbers and dividing it by the total number of numbers in the set. This mathematical calculation provides a representative value that can be used to describe the central tendency of the data.
In this article, we will explore the complete information about the average in math and stat. We will discuss how an average can be used to gain valuable insights from data. By practical examples, readers will gain a solid understanding of how averages can be calculated and what are the purposes of finding averages in various fields.
What is Average?
The term average refers to a measure that represents a central tendency of a set of numbers. Let us illustrate these words in detail:
The calculation of the individual sum of the data elements divided by the total number of elements in the data set is known as the average of a data set. This is also known as the mean value and is commonly used to represent the central tendency of a dataset.
Average Symbol
The symbol used for average or mean value is x̅ or simply μ (mu).
Average Formula
We can calculate the average value of any collection of terms with the use of the average formula:
Average = Total Sum of all terms in the set ÷ total no. of terms in the set
Mathematically,
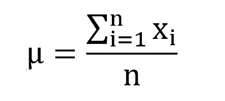
Where
- ∑ is the summation symbol,
- xi describes all elements of a set,
- n is the total number of elements of the set.
Types of Average
In terms of statistics, there are three particular types of averages including Mean, Median, and Mode. In this section, we will discuss all of these types in detail with their definitions and formulas.
Mean
The mean represents the description of the sum of all values divided by the number of values. It is typically referred to as the average.
Mean = μ = ∑xi /n = (x1 + x2 + … + xn)/n
For example, the mean of the numbers {1, 2, 3, 4, 5} is (1+2+3+4+5)/5 = 3.
Median
When values are arranged in numerical order in a dataset, the middle value is called the median.
Mathematically, if n represents the number of values in the dataset, the formula to find the median is:
If n is odd: Median = (n+1) ÷ 2
If n is even: Median = [(n/2) + (n/2 + 1)] ÷ 2 = 1st middle value + 2nd middle value/ 2
For example, the median of the numbers {1, 2, 3, 4, 5} is (5+1)/2 = 3.
The median of the numbers {3, 4, 5, 6} is (4 + 5)/2 = 4.5
Mode
The mode is the value that the greatest number of times appears in a dataset. A dataset can contain one or more modes or no mode at all.
For example, in the dataset {1, 2, 2, 3, 4, 4, 4} the mode is 4.

Significances of Average
The average significance lies in its ability to help us understand large amounts of data by providing a single value that represents the data set.
Here are some of the significances of the average:
- Average shows a measure of central tendency:
The average provides a representative value that carries the central tendency of the data.
- Average helps make comparisons:
Comparing two or more sets of data becomes easier when we have a single average value for each set.
- Average makes simpler data performance:
The use of average enables data to be presented concisely and simply.
- Average helps statistical analysis:
The average is an essential calculation when it comes to performing further statistical analysis. It can be used as a basis for other metrics such as variance, standard deviation, and correlation coefficients.
- Average can be used for prediction:
Future trends and outcomes can be predicted using the average of past data.
Overall, the average is a powerful tool in statistics and is used in many fields such as finance, economics, medicine, and engineering.
Use Calculator: SGPA Calculator
Steps for calculating average
To find the average of any data set, we just do a simple calculation according to the average formula.
Here is the step-by-step tutorial to calculate the average term:
- Sum all the terms in the dataset.
- Counting how many terms are in the dataset.
- Divide the total sum by the number of terms in the dataset.
In examples, you will see how we apply these steps in practical life and find their average points.
Examples
- IQ level of a group of math students as 99, 121, 108, 132, 110, and 139. What is the average IQ score of the group?
Solution: Given that the group IQ scores as 99, 121, 108, 132, and 139. We can see that there are five students in the group whose IQs have been tested. Let us find their average score.
Step 1: Sum all the terms together:
= 99 + 121 + 108 + 132 + 139
= 570
Step 2: Count the Number of values:
N = 5
Step 3: Divide the sum by the count:
570/5 = 114
The math students got an average IQ score of 114.
- A 10-floor building has the capacity for guests as per floors 100, 95, 90, 85, 80, 75, 70, 65, 60, and 55. Find out the average capacity of each floor.
Solution: Given that the capacity of every floor: {100, 95, 90…, 55}
Let us suppose:
{100, 95, 90…, 55} = (x1, x2…, x10)
Average formula = ∑xi/n
Step 1:
∑i=110 xi = (x1 + x2 + … + x10)
= {100 + 95 + 90 + 85 + 80 + 75 + 70 + 65 + 60 + 55}
= 775
Step 2:
Number of floors.
n = 10
Step 3:
Average = ∑xi /n
= 775/10
= 77.5
The average capacity for the guests is 77.5 persons per floor.
An average calculator can also be used for finding the average of the given set of data values to get results in a matter of seconds.
Wrap Up
This article contained a complete understanding of averages in math and stats. It explained different types of averages and their formulas. In this lesson, we taught how to calculate the average value by following simple steps.
The main advantage of using the average is that it allows the summarizing of large amounts of data with a single value that represents the central tendency of the data set. By reviewing practical examples, readers can get an effective grasp of the concept of average as a powerful tool for data analysis and interpretation.





